Unit 1 Advanced Abstract Algebra Pdf Group Mathematics Geometry

Unit - 1 Advanced Abstract Algebra | PDF | Group (Mathematics) | Geometry
Unit - 1 Advanced Abstract Algebra | PDF | Group (Mathematics) | Geometry Although this course assumes familiarity with the topics in a typical undergraduate course on abstract algebra, including subgroups, normal subgroups, homomorphisms, quotient groups, etc., we will start with a quick review. After that, we study the properties of cosets leading to the normal subgroups, the order of an element and related properties, group homomorphisms, isomorphisms, etc. group theory is very vast and cannot be limited to one unit.

Abstract Algebra: 1 Semigroups | PDF | Group (Mathematics) | Mathematical Structures
Abstract Algebra: 1 Semigroups | PDF | Group (Mathematics) | Mathematical Structures Unit iv : vector spaces – linear transformation and bases – algebra of linear transformations – form triangula trace & tanspose. It is clear that this process allows you to label each eld: 1=1 is number 1, 1=2 is number 2, 2=1 is number 3, and so on. so, the set of all squares is in bijection with the set n. This text is intended for a one or two semester undergraduate course in abstract algebra. traditionally, these courses have covered the theoretical aspects of groups, rings, and elds. These are notes which provide a basic summary of each lecture for math 331 1, the rst quarter of \menu: abstract algebra", taught by the author at northwestern university.

Abstract Algebra | PDF | Group (Mathematics) | Matrix (Mathematics)
Abstract Algebra | PDF | Group (Mathematics) | Matrix (Mathematics) This text is intended for a one or two semester undergraduate course in abstract algebra. traditionally, these courses have covered the theoretical aspects of groups, rings, and elds. These are notes which provide a basic summary of each lecture for math 331 1, the rst quarter of \menu: abstract algebra", taught by the author at northwestern university. This is the idea behind abstract algebra. the present course is the study of a \group," which is a set with an asso ciative operation, having an identity element, and such that each element has an inverse (see section 4). with some restrictions, each of the examples above gives rise to a group. They cover topics in group theory including the definition of groups, subgroups, groups of permutations, cosets, homomorphisms, rings, integral domains, and vector spaces. the notes are intended to help students learn the concepts and do practice problems to better understand abstract algebra. These are lecture notes for a year long graduate course in abstract alge bra given at the university of oregon in 2002 2003. the text is advanced modern algebra by j. rotman. i will greatly appreciate if you will let me know of any misprints or errors you can find in these lecture notes. An introduction to group theory. various classes of groups are studied: symmetric groups, abelia. , cyclic, and permutation groups. basic tools are developed and used: subgroups, normal subgroups, cosets, the lagrange theorem, group homomorphisms, quotient groups, direct pro. ucts, and group actions on a set. the course culminates with the sylo.

Algebra 1 | PDF | Group (Mathematics) | Function (Mathematics)
Algebra 1 | PDF | Group (Mathematics) | Function (Mathematics) This is the idea behind abstract algebra. the present course is the study of a \group," which is a set with an asso ciative operation, having an identity element, and such that each element has an inverse (see section 4). with some restrictions, each of the examples above gives rise to a group. They cover topics in group theory including the definition of groups, subgroups, groups of permutations, cosets, homomorphisms, rings, integral domains, and vector spaces. the notes are intended to help students learn the concepts and do practice problems to better understand abstract algebra. These are lecture notes for a year long graduate course in abstract alge bra given at the university of oregon in 2002 2003. the text is advanced modern algebra by j. rotman. i will greatly appreciate if you will let me know of any misprints or errors you can find in these lecture notes. An introduction to group theory. various classes of groups are studied: symmetric groups, abelia. , cyclic, and permutation groups. basic tools are developed and used: subgroups, normal subgroups, cosets, the lagrange theorem, group homomorphisms, quotient groups, direct pro. ucts, and group actions on a set. the course culminates with the sylo.

PDF | PDF | Group (Mathematics) | Abstract Algebra
PDF | PDF | Group (Mathematics) | Abstract Algebra These are lecture notes for a year long graduate course in abstract alge bra given at the university of oregon in 2002 2003. the text is advanced modern algebra by j. rotman. i will greatly appreciate if you will let me know of any misprints or errors you can find in these lecture notes. An introduction to group theory. various classes of groups are studied: symmetric groups, abelia. , cyclic, and permutation groups. basic tools are developed and used: subgroups, normal subgroups, cosets, the lagrange theorem, group homomorphisms, quotient groups, direct pro. ucts, and group actions on a set. the course culminates with the sylo.
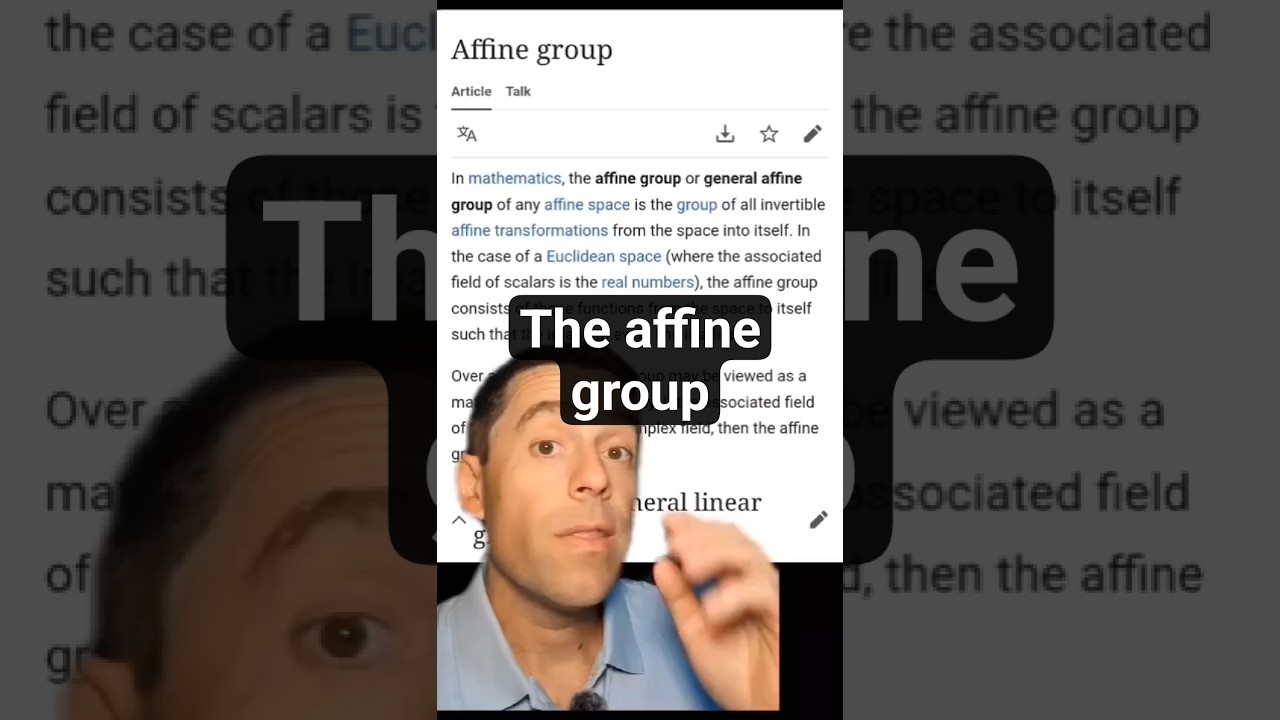
The affine group in abstract algebra #math #abstractalgebra #grouptheory #geometry #stem
The affine group in abstract algebra #math #abstractalgebra #grouptheory #geometry #stem
Related image with unit 1 advanced abstract algebra pdf group mathematics geometry
Related image with unit 1 advanced abstract algebra pdf group mathematics geometry
About "Unit 1 Advanced Abstract Algebra Pdf Group Mathematics Geometry"
















Comments are closed.